Vida Artificial

VIDA ARTIFICIAL

“La vida es un proceso de información” (John von Neumann)

“La vida ocurre en un tablero de damas virtual. Las casillas se llaman células” (John Conway)

“Queremos crear vida en la computadora y no en tubos de ensayo” (Christopher Langton)

“La vida es un software en evolución” (G. Chaitin)

La Vida Artificial
La vida artificial −abreviadamente, VA en español, AL o ALIFE en inglés− es un campo relativamente nuevo que trata de simular los procesos biológicos mediante métodos informáticos (computacionales). La VA es el estudio de la vida en el ambiente digital.

Según Christopher Langton −el primero en utilizar el término “vida artificial”− la VA es “el campo de estudio dedicado a la comprensión de la vida, intentando abstraer los principios dinámicos fundamentales que subyacen a los fenómenos biológicos, y recreando esas dinámicas en otros medios físicos tales como ordenadores haciéndolos accesibles a nuevos tipos de manipulación experimental y de pruebas”.

La VA nació por la necesidad de una biología teórica, de tipo computacional, basada en leyes universales. Sus objetivos son:

Determinar las características que definen los procesos vivos, independientemente del sustrato, de la materialidad en la que tienen lugar. Incluye la cuestión de si la vida es dependiente de algún medio o materia particular.
Investigar los mecanismos que hacen emerger “lo vivo” como un fenómeno no reducible a sus componentes.
Simular por ordenador el comportamiento autónomo de los seres vivos. Un ser vivo artificial encapsula una paradigma: una visión del mundo, unos sentidos, unas creencias y unos objetivos.
Explorar formas alternativas de vida. Según Langton, “la VA trata de situar la vida 'tal como es' dentro del contexto de la vida 'tal como podría ser'”.
Gestionar el tiempo de los organismos virtuales. La diferencia entre un organismo vivo y uno virtual es la posibilidad de manipular el tiempo: se puede acelerar o retardar.
Practicar la biología sintética a partir de componentes, en analogía con la química sintética.

Los autómatas celulares

La VA nació con los autómatas celulares (ACs). Un AC es un tipo de autómata finito que consta de:

Una malla bidimensional de casillas cuadradas (tipo tablero de damas o ajedrez) que representa el “espacio biológico” y en donde una casilla negra representa una célula viva y una casilla blanca representa una célula muerta o un espacio sin vida. Esto es generalizable a más de dos estados.
Un conjunto de reglas simples que establecen cómo va a evolucionar el sistema, es decir, si las casillas permanecerán en el mismo estado o cambiarán de estado.
El sistema evoluciona de manera discreta, discontinua, donde todas las casillas de cada generación se calculan a la vez, de manera sincrónica.

El hecho de que unas reglas simples pueden producir comportamientos extraordinariamente complejos, hacen de los ACs un posible fundamento teórico de la vida y, por extensión, de la inteligencia. En efecto, los ACs permiten simular las funciones de: interacción con el entorno, evolución, así como coexistencia y competitividad de varias formas de vida compartiendo el mismo medio.

Los ACs fueron ideados por Stanislaw Ulam, pero fue John von Neumann quien los impulsó como modelo computacional al utilizarlos para implementar una máquina teórica capaz de autorreproducirse. A von Neumann se le considera “el padre” de la VA.

Von Neumann denominó a las máquinas autorreproductoras “Universal Assemblers”. Uno de los conceptos que definió fue el de “constructor universal”, un dispositivo capaz de construir otra máquina idéntica a partir de su propia descripción estructural y constructiva, un mecanismo que también poseen las células, que contienen, no solo información sobre su estructura, sino también sobre cómo construir otras células del mismo tipo. En principio, la máquina autorreproductora de von Neumann se consideró una tarea imposible, sobre la base de que tal máquina debería contener una descripción de sí misma, y que esta descripción necesitaría también una descripción, y así hasta el infinito.

En unas conferencias que dio en Princeton en 1948, von Neumann decía que un máquina autorreproductora tendría que tener por lo menos 8 clases distintas de piezas: 4 para el cerebro y 4 para la parte motora. Su máquina llegó a tener 29 estados por célula (estados identificados según su funcionalidad) y una sola regla de transición, pero no llegó a finalizarla debido a su prematura muerte. Desde entonces se han hecho varios intentos, sin éxito, de completar su trabajo.

Von Neumann demostró que una máquina puede crear otra máquina más complicada que sí misma. Puede haber generaciones de máquinas, cada una más compleja que sus predecesoras. Es lo mismo que sucede en la evolución biológica. Von Neumann demostró que incluso la complejidad de los organismos vivos se puede reducir o compactar en un conjunto relativamente simple de reglas recursivas. La auto-reproducción se puede entender como la consecuencia de una “física” simplificada basada en un autómata celular. Según von Neumann, la reproducción biológica es mecanicista y se puede formular una definición de la vida en términos de información.

Según Ed Fredkin: El universo es realmente un ordenador gigantesco, concretamente un AC gigantesco. Los ACs son, en esencia, mundos no diferentes al nuestro. Existe un proceso de información que subyace a todo. “Si algo no se puede hacer en un ordenador, entonces no podemos hacerlo mediante un proceso puramente mecánico”. Y los organismos vivos que habitan este universo operan bajo los mismos principios que los procesos computacionales.

El juego de la vida

El “juego de la vida” fue inventado por John Conway en 1970 cuando trataba de simplificar drásticamente las reglas y los estados de la máquina autorreproductora de von Neumann. Es un autómata celular bidimensional que representa el paradigma de la complejidad dinámica a partir de lo simple: tres reglas muy simples aplicadas sucesivamente (a una configuración inicial de células negras) pueden producir resultados dinámicos extremadamente complejos. Las reglas son las siguientes:

Si una celda negra tiene 2 ó 3 vecinas negras, permanece negra (sobrevive).
Si una celda blanca tiene 3 vecinas negras, se convierte en negra (revive).
En el resto de los casos, la celda permanece blanca (si es blanca) o se convierte en blanca (si es negra).

Regla	Antes	Después
1. Una célula viva con 2 o 3 células vecinas vivas sobrevive
2. Una célula muerta con 3 células vecinas vivas revive
3a. Una célula viva con menos de 2 células vecinas vivas muere
3b. Una célula viva con más de 3 células vecinas vivas muere

Características:

El juego se desarrolla sobre un tablero virtual infinito.
Es un juego de un solo jugador. Interviene únicamente al principio del juego, al establecer la forma inicial. A partir de ese momento, el juego es automático, pues su evolución está determinada por dicha forma inicial.
Las células negras representan a las células vivas y las blancas a las células muertas. Cada célula tiene 8 células vecinas.
La forma inicial evoluciona en tiempos discretos, donde todas las células se actualizan a la vez.
Aparecen propiedades emergentes globales y auto-organizativas inducidas por la dinámica local.
Las formas iniciales evolucionan de manera sorprendente. La mayoría de las formas simples evolucionan hacia formas estables. Otras formas evolucionan a configuraciones periódicas oscilantes. Algunas formas iniciales simples tienen una vida muy compleja, siendo el “pentominó r” el ejemplo más representativo: esta forma es un grupo de células contiguas que recuerda a la letra “r”, que se estabiliza tras 1103 generaciones.

Pentominó-r
Permite emular la máquina universal de Turing, es decir, todo lo que puede computar una máquina de Turing lo puede computar el juego de la vida. También puede emular cualquier modelo computacional. Un ordenador abstracto se puede construir con patrones del juego de la vida.

El juego de la vida es el mejor ejemplo de autómata celular y la aplicación paradigmática de los procesos biológicos computacionales. Contribuyó de forma decisiva en la difusión del concepto de AC, convirtiéndose en motivo de inspiración para los investigadores. Debido a la simplicidad de las reglas y la enorme cantidad de formas dinámicas que puede generar, el juego despertó un gran interés y se hizo popular casi instantáneamente, convirtiéndose incluso en objeto de culto durante los años 1970s y posteriores. Era fácil experimentar mediante el ordenador personal, se podía ver en la pantalla cómo evolucionaba un “ser vivo” artificial. Fue también el precedente de los fractales, pues algunas formas recuerdan a estas formas geométricas recursivas.

He aquí un ejemplo de una configuración oscilante de periodo 3:

A Christopher Langton le cautivó el juego dela vida de Conway. Desde que lo conoció, persiguió la idea de que era posible simular criaturas vivas en el ordenador. Tras años de estudio, intentó simplificar el AC de von Neumann, de 29 estados a solo 8. En 1979 consiguió el primer organismo computacional autorreproductor usando un ordenador personal.

La visión de Wolfram

Wolfram mostró en su libro “A New Kind of Science” que los ACs permiten generar muchas formas complejas a partir de reglas determinísticas muy simples aplicadas recursivamente. Que los ACs permiten crear un nuevo tipo de ciencia para modelar los fenómenos físicos, una alternativa más simple, directa y visual que las crípticas ecuaciones diferenciales. Wolfram exploró y categorizó los tipos de complejidad que producen los ACs y mostró cómo podían modelar las formas de la naturaleza como las conchas marinas y el crecimiento de las plantas. Wolfram veía el ordenador como un territorio abstracto ideal para la experimentación, y los ACs como el sistema más simple y potente.

Las bioformas de Richard Dawkins

Las bioformas (biomorphs) son criaturas digitales producidas por ordenador por Richard Dawkins, que las describe en el capítulo 3 de su libro de 1986 “El relojero ciego” [1993], un texto de divulgación del neodarwinismo, del que es defensor. Dawkins escribió el programa (que denominó “Evolution”) para ilustrar como se pueden crear bioformas significativas complejas sin necesidad de un diseñador. Las bioformas constituyen un puente entre el neodarwinismo y la VA.

Una bioforma es un gráfico 2D, tipo árbol, generado por un algoritmo recursivo, que se reproduce y muta como un ser vivo. Inicialmente, el gráfico es muy simple, pero tras un cierto número de pasos (recursiones) puede convertirse en un gráfico muy complejo. La bioforma madre inicial es un segmento de recta vertical. De este segmento se ramifican otros segmentos, y de estos otros segmentos, y así sucesivamente hasta completar todas las recursiones previstas.

Una bioforma tiene 9 genes (numerados del 1 al 9). Cada gen representa un aspecto o parámetro de la bioforma. Puede tomar un valor entero entre −9 y +9. Dawkins no explicó con detalle los parámetros, pero dio algunas pistas como el número de ramas, longitud de cada rama y el ángulo de ramificación. El último gen (el 9°) es la profundidad de la recursión. Los genes de la bioforma reflejan el aspecto externo (el fenotipo) y su evolución, de forma análoga a lo que ocurre con los genes biológicos. Puesto que hay 9 genes y 19 valores posibles para cada gen, el número de diferentes bioformas posibles es 19¹⁹. E el Apéndice I de su libro, Dawkins presentó una ampliación del algoritmo con 16 genes en lugar de 9.

El proceso evolutivo de una bioforma es el siguiente:

Se parte de una bioforma madre inicial basada en valores aleatorios de los genes. Aparece en el centro de una matriz de 3×3 elementos, es decir que está rodeada de 8 casillas. En la siguiente generación, en estas 8 casillas aparecen 8 mutaciones de la bioforma madre, cada una con solo un gen modificado en una unidad (positiva o negativa). Los genes mutados se seleccionan al azar, así como también el signo del incremento unitario. Cada una de las formas hijas no son idénticas a la madre, pero guardan un parecido, puesto que solo muta un gen en cada una de ellas. Las mutaciones se dice que son “locales”.

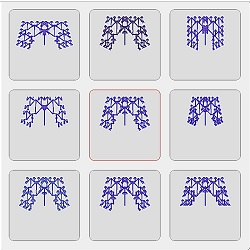
Una bioforma y sus
8 descendientes
De las 8 bioformas descendientes, el controlador humano decide qué descendiente sobrevive, de acuerdo con algún criterio (de tipo estético, por el parecido a una forma deseada, etc.). El controlador humano desempeña así el papel de la naturaleza, convirtiéndose en “criador”.
El descendiente superviviente se convierte en la nueva bioforma madre de la generación siguiente. Ocupará el centro de la matriz y generará 8 mutaciones. Y así sucesivamente hasta alcanzar el número de recursiones previstas. La apariencia final (fenotipo) emerge de la cadena evolutiva y los cambios acumulados del “código genético” (la secuencia de valores de los genes) de la bioforma, y puede llegar a ser muy compleja. Cada gen de una bioforma contribuye a un aspecto y está presente en todos los niveles del dibujo.

Selecionando en cada generación la forma que más se aproxime a lo que se desee obtener, puede lograrse cualquier cosa.

Cuando Dawkins ejecutó su programa evolutivo de bioformas, se quedó sorprendido de la gran variedad de formas que aparecían, que recordaban a formas biológicas del mundo real como insectos, árboles, flores, arbustos, escarabajos, mariposas, arañas, ranas, escorpiones, murciélagos, etc.. Pero también aparecían formas no-biológicas como templos aztecas, ventanas de iglesias góticas, balanzas, copas, e incluso letras del alfabeto. Entonces Dawkins tomó conciencia de que había creado un universo de formas al que denominó “Biomorph Land”.

Dawkins vio que, para construir un universo biológico práctico, tenía que restringir las formas posibles a solo aquellas que tenían un sentido biológico interesante. Una de las restricciones que utilizó, por razones estéticas (y también para economizar el número de genes necesarios), fue establecer una simetría izquierda-derecha, el mismo criterio que se utiliza en el test de Rorschach de las manchas de tinta.

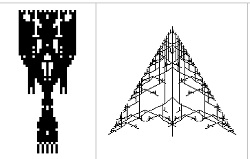
Santo Grial y Árbol de Navidad

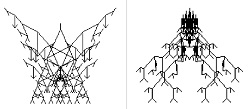
Diablo y La reina de las arañas

En una de sus incursiones por este universo, llegó por casualidad a un patrón en forma de cáliz que le cautivó sobremanera y que denominó “Santo Grial” (ver figura), pero no consiguió recuperar la secuencia de cambios para su generación. Ofreció 1000$ de premio a la persona que consiguiera generarlo. Thomas Reed (un ingeniero de software de California) lo encontró y ganó el premio. Pocas semanas después otros dos buscadores, de manera independiente, también lo encontraron.

Con su programa de generación de bioformas, Dawkins pretendía demostrar:

La evolución es un proceso gradual y acumulativo basado en el azar y el mecanismo de selección. El azar crea la variabilidad. La selección es la que hace que la evolución vaya en una cierta dirección de mejora. Las pequeñas mejoras realizadas sobre muchas generaciones hacen que sea imposible reconocer al progenitor original. La selección aleatoria nunca produce un diseño coherente, pero sí la selección acumulada según un cierto criterio.
La evolución es fundamentalmente un proceso no-aleatorio. El azar es solo el “combustible” del proceso. La selección acumulativa (y no aleatoria) es el factor creativo e impulsor de la evolución.
No existe una gran diferencia entre la selección natural y la artificial. En la selección natural es la naturaleza la que decide en función de su adaptabilidad al entorno. En la selección artificial hay un criador decidiendo qué descendiente sobrevive en cada generación.
La complejidad que se encuentra en el mundo natural no necesita un diseñador inteligente. La complejidad puede emerger mediante acumulación progresiva de pequeñas modificaciones. Se muestra así el postulado de Darwin de que los organismos complejos se forman gradualmente mediante pequeños cambios acumulativos.

Un reloj lo crea un relojero de manera consciente, para un propósito. Pero el cosmos y el hombre ha sido creados sin ningún propósito, por las fuerzas ciegas, inconscientes y automáticas de la selección natural: el “relojero ciego”.
A nivel molecular, los organismos obedecen las leyes de la física, pero a gran escala, no la obedecen. La vida es un fenómeno emergente.
Una única forma primigenia −el segmento vertical, en el caso de las bioformas− puede ser el origen de todas las formas. Se muestra así la hipótesis de Darwin de que todos los seres vivientes descienden de un antecesor común.
El proceso recursivo utilizado en la generación de bioformas también se produce en los embriones de los seres vivos. Todos los embriones crecen por división celular (una célula se divide en dos células hijas) y la forma final del organismo emerge como consecuencia de muchos pequeños cambios celulares locales.

Las bioformas de Dawkins y sus conclusiones han recibido varias críticas. La principal se basa en que un mecanismo de selección que requiere un agente humano no puede ser darwiniano. A ello responde Dawkins que la selección utilizada no es natural sino artificial. A esto se objeta que la selección no debe de calificarse como artificial sino como humana.

Características de la VA

Investigación.
La VA trata de describir qué es exactamente la vida; si la vida es algo que depende de un soporte físico o si se trata de algo independiente del soporte físico y basado solo en estructuras de información.

El carácter interdisciplinar que exige la investigación de la vida, hace que la VA sea un punto de encuentro de muchas disciplinas: biología, física, filosofía, matemática, informática, lógica, lingüística, cibernética, teoría general de sistemas y dinámica de sistemas.
Simulación.
La VA puede adoptar dos formas de simulación:
1. La sintética. Se basa en la construcción de dispositivos constituidos por elementos mecánicos que tratan de simular a los sistemas vivientes. En este apartado hay que incluir a los robots.
2. La virtual (o computacional). Se basa en el desarrollo de sistemas simbólicos sin soporte mecánico e implementables en un ordenador mediante estructuras de información. Esta forma de simulación proporciona un marco de estudio inmejorable del estudio de los fenómenos de la vida por su simplicidad, flexibilidad y facilidad de implementación, trascendiendo las limitaciones de las observaciones científicas. Este segundo aspecto es el que más nos interesa aquí.
LA VA no es una ciencia empírica en sentido tradicional. Su campo de experimentación es el ordenador, el mundo informático, no el mundo natural.
Tipos de VA.
Una cuestión clave es si lo que generamos en el ordenador posee algunas características de la vida. ¿El modelo computacional es el medio para el estudio de la vida o es la realidad profunda y abstracta que subyace a todo fenómeno biológico? ¿Tienen vida realmente los seres digitales?

Tom Ray −autor del programa Tierra− sostiene que no está simulando vida en un ordenador, sino que la está sintetizando.

Según Heinz Pagels, “El modelo computacional es la realidad, no un medio para estudiarla”.

Según Ed Fredkin, “Si un ordenador no puede hacer algo, la naturaleza tampoco”.

Según Christopher Langton, “Queremos crear la vida en la computadora, no en tubos de ensayo”.

La VA “fuerte” es la visión que sostiene que es posible realmente crear la vida mediante la simulación, que es una realidad (virtual) que tiene el mismo estatus ontológico que el mundo real, puesto que se trata de un medio físico real y usando recursos físicos reales. Langton es defensor de la VA fuerte: las simulaciones de los seres vivientes tienen vida, aunque reconoce que esta cuestión es indemostrable.

La VA “débil” niega que sea posible crear vida, pero que es posible simular los procesos de la vida en el ordenador mediante técnicas como los ACs, algoritmos evolutivos, algoritmos genéticos, programación orientada a agentes, redes neuronales, lógica borrosa, etc. Las redes neuronales intentan simular el funcionamiento del sistema nervioso. Los algoritmos genéticos tratan de imitar la selección natural mediante la mutación y entrecruzamiento de material genético.
Ciencia de la complejidad.
La VA está incluida en las llamadas “Ciencias de la Complejidad”, que estudia los fenómenos subyacentes comunes a todos los sistemas complejos modelados mediante interacción de elementos simples. Ilya Pigogine es considerado uno de los fundadores. El principal centro de investigación de los sistemas complejos es el Santa Fe Institute (SFI), fundado en 1984, uno de cuyos fundadores es el físico Murray Gell-Mann (el proponente del modelo de los quarks para el núcleo atómico).
Diferencia con la IA.
La VA es un campo de estudio independiente de la Inteligencia Artificial (IA). La IA es a la psicología como la VA es a la biología. El objetivo de la IA es simular la inteligencia humana. El objetivo de la VA es simular el comportamiento de los seres vivos. No obstante, la frontera entre ambas disciplinas es, a veces, difusa.
Diferencia con otras disciplinas.
La VA es diferente de otras disciplinas más o menos relacionadas:
- La ingeniería genética o biología sintética, que está basada en el ADN de la materia orgánica.
- La biolingüística estudia las analogías entre los sistema lingüísticos y biológicos.
- La bioinformática es la aplicación de la informática para la gestión de la información de los sistemas biológicos.
- La biología matemática o biomatemática desarrolla modelos matemáticos de los procesos biológicos.
- La biología teórica tiene por objeto la caracterización conceptual de problemas biológicos y su formalización mediante modelos matemáticos y simulaciones informáticas.
- La biocibernética. Es la ciencia de la comunicación y control entre los organismos vivos y su interacción con los sistemas mecánicos o electrónicos.
- La biología computacional desarrolla modelos teóricos computacionales de los sistemas biológicos.
- La biocomputación o bioinformática es la computación con la ayuda de algún componente de tipo biológico. Es equiparable a la denominada “computación natural”, como la computación con moléculas de ADN y computación celular con membranas.
- La biología evolutiva del desarrollo (Evolutionary Development Biology o EvoDevo Biology) es una disciplina iniciada por D’Arcy Thompson que tiene por objeto descubrir patrones de auto-organización en los organismos.

Los desafíos de la VA

La VA es una disciplina joven y tiene por delante muchos retos, entre ellos los siguientes:

Entender la naturaleza de la vida, la evolución y los fenómenos emergentes. Descubrir las leyes fundamentales de la evolución y la complejidad biológica. Ver si la vida es un concepto universal que puede aplicarse más allá del dominio de la biología. ¿Es el cosmos un ser viviente? ¿En qué sentido se puede decir que ciertos entes (como la sociedad, los mercados financieros, etc.) tienen vida? ¿Hay grados de vida o la vida es de naturaleza discontinua?
Proporcionar a la VA un fundamento mediante el desarrollo una teoría de la información unificada, abstracta y coherente de los sistemas vivientes evolutivos, en los aspectos de generación de información, proceso de información y transmisión de información. La vida debería comprenderse mejor a nivel informacional, abstracto, simbólico y computacional. ¿Cómo se generan nuevas reglas (y reglas de orden superior) y estructuras simbólicas para formalizar la evolución?
Crear un modelo formal para la vida que rige en todos los niveles de la vida: bacterias, células, órganos, etc. Este es el Santo Grial de la VA.
Investigar las características comunes a todos los procesos evolutivos. Y si existen clases de procesos evolutivos.
Producir y entender los procesos evolutivos de complejidad creciente continua e ilimitada (open-ended evolution).
Investigar si los sistemas digitales tienen el mismo potencial de innovación o creatividad evolutiva que los seres vivientes.
Investigar cómo se comunican e interaccionan los niveles jerárquicos de los seres vivientes a nivel local y no-local.
Investigar si es posible que emerja mente e inteligencia en un sistema viviente artificial.
Investigar formas de vida alternativas, pues pueden ayudar a entender el fenómeno de la vida natural.
Investigar la relación entre IA y VA, la relación intrínseca entre seres vivientes artificiales y la inteligencia artificial. ¿Es más beneficioso estudiar la IA en el contexto de la VA? ¿Puede emerger IA a partir de la VA?

Analogías entre IA y VA

La VA está muy relacionada con la IA porque los sistemas vivientes artificiales pueden exhibir un cierto grado de inteligencia. Además, existen ciertas analogías entre ambas disciplinas. En varios aspectos se pueden considerar disciplinas complementarias.

Ambas son de carácter interdisciplinario y hacen uso de los mismos recursos computacionales. Ambas promueven la generalización y la abstracción para ayudar a comprender la psicología y la biología, respectivamente.
La VA tiende a usar modelos de bajo nivel, de tipo abajo-arriba (bottom-up) en el que el comportamiento global emerge indirectamente mediante recursión computacional, comportamiento que puede ser difícil de prever. Los elementos son simples, y las reglas con las que interactúan los elementos son también simples. En la VA, como los sistemas complejos en general, no existe un control centralizado, aunque pueden existir condiciones de contorno.

La IA usa modelos arriba-abajo (top-down) para lograr directamente el comportamiento deseado y previsto (como, por ejemplo, los sistemas expertos). La complejidad se programa directamente en los elementos. En los modelos de IA suele haber un control centralizado.
LA IA nació en el Dartmouth College en 1955. John McCarthty fue el primero en utilizar el término “inteligencia artificial”. La VA nació en Los Alamos National Laboratory en 1987. Christopher Langton fue el primero en utilizar el término “vida artificial”.
En ambas disciplinas se habla de versiones “fuerte” y “débil”.
El test de Turing tiene versión IA y versión VA.
Turing propuso su famoso test para determinar si una máquina era capaz de emular la mente humana. Se basa en el intercambio de mensajes entre una persona y una máquina. La persona envía mensajes con sentido. La máquina trata de responder a esos mensajes de manera coherente, con la ayuda de reglas sintácticas. El test de Turing pone énfasis en la capacidad lingüística, pero no tiene en cuenta las capacidades robóticas, de movimiento asociadas a la vida. Un test de Turing que incluya este último aspecto es un test de Turing generalizado.

Langton ha formulado un test en la VA, análogo al test de Turing para la IA, que ha sentado las bases para fundamentar la vida sobre la informática teórica.

MENTAL y la Vida Artificial
Vida natural, artificial y abstracta

Hay que distinguir entre tres tipos de vida:

La vida natural (o real) es la vida de los organismos vivientes.
La vida artificial es la vida simulada por un ordenador, que está limitada por la física (la electrónica). La vida artificial solo puede reflejar la complejidad del mundo físico artificial en el que “vive” el organismo.
La vida abstracta (o formal) es independiente de la implementación y no está limitada porque pertenece al mundo mental.

De estas tres categorías, la más profunda es la abstracta, seguida de la artificial, y por último la natural.

Análogamente, puede hablarse también de física natural (la del mundo real), física artificial y física abstracta. La física artificial es la que puede simularse en un ordenador, es la física como es y como podría ser. La física abstracta es independiente de toda implementación.

Respecto a la computación, hay que distinguir tres tipos:

La computación natural se refiere a la forma en que las leyes de la naturaleza producen modificaciones en determinados sistemas, que pueden interpretarse como procesos computacionales. Dentro de la computación natural se incluyen, entre otros, la computación con moléculas de ADN y la computación celular con membranas.
La computación artificial (o física) es la que se realiza en un ordenador, que es dependiente del hardware utilizado y está limitada por las leyes de la física que gobiernan el hardware. Los ordenadores de la arquitectura von Neumann, aunque inspirada en la máquina de Turing, son de este tipo.
La computación abstracta o formal, que es independiente de la implementación porque es de tipo mental. Las operaciones matemáticas que habitualmente realizamos (la manipulación formal de símbolos) son de este tipo. La máquina de Turing, que es un dispositivo teórico y abstracto, también es de este tipo. Paradójicamente, los procesos computacionales (los que puede realizar una máquina de Turing) se denominan “efectivos” o “mecánicos”, a pesar de que no tienen relación con el mundo físico.

La computación ideal es una computación e la que existe un isomorfismo entre la computación artificial y la abstracta. Cuando se reemplaza el isomorfismo por la identidad tenemos computacionalismo (o filosofía computacionalista). Es el caso de un hipotético ordenador cuyas primitivas sean las primitivas de MENTAL. En MENTAL confluyen la física abstracta, la mente abstracta, la computación abstracta y la vida abstracta.

Según la teoría “it from bit” de John Wheeler, en lo más profundo de la realidad está la información (el bit). El mundo superficial conocido (el it) es una manifestación de la información. La computación pertenece al nivel profundo de la realidad. El universo es una representación, mapa o representación superficial de un proceso profundo que es la computación. El universo es un computador que lleva millones de años calculando algo que la ciencia trata de descubrir.

Los arquetipos y la vida abstracta

El lenguaje verdaderamente es la clave de todo, como lo es de la conciencia. La vida es la manifestación de la conciencia sobre la materia y cuyo resultado es una unidad organizada e interrelacionada. La vida abstracta está basada en los arquetipos de la conciencia.

Los arquetipos abstractos de la conciencia son universales y se manifiestan en todos los planos de la realidad, incluido el plano de la vida. Las manifestaciones de los arquetipos abstractos permiten generar vida abstracta de forma auto-referencial, cerrada, para generar formas autónomas. Las funciones biológicas son arquetipos manifestados.

Al compartir los mismos arquetipos, la lingüística se une con la biología. Toda unión debe hacerse desde lo profundo, desde los arquetipos.

El lenguaje de la vida es el mismo que para la mente y para la naturaleza: MENTAL, pues se basa en los mismos arquetipos de la conciencia manifestados en estos planos.

Respecto a la cuestión planteada de si los procesos computacionales (que simulan la vida) son o no la realidad, hay que decir que lo computacional está en un nivel profundo, abstracto, más allá de lo físico y mental. Cuando lo computacional se expresa mediante los arquetipos primarios, estamos en el nivel más próximo a la conciencia, es decir, en el nivel más próximo a la vida. Los arquetipos primarios se manifiestan en todos los niveles. MENTAL es un modelo de la mente, de la conciencia y de la vida. MENTAL es un ordenador universal que se manifiesta en todos los niveles de la realidad. Es un modelo universal.

MENTAL, un lenguaje para la VA

En la VA confluyen muchas disciplinas, pero la mejor forma de estudiarla es mediante los mecanismo comunes a todas ellas, que son los arquetipos primarios. Las ventajas de este enfoque son:

Integra el principio de causalidad ascendente (PCA) y el principio de causalidad descendente (PCD).

MENTAL es un lenguaje basado en el PCD. Pero en los fenómenos de emergencia (como en el juego de la vida) aparece el PCA.
Simplificación.
Supone una extraordinaria simplificación de los modelos teórico-prácticos. Ocurre lo mismo que con la IA, en la que los desarrollos también se simplifican notablemente. La simplificación se debe a la potencia de los arquetipos primarios en general, pero particularmente al poder de las expresiones genéricas y sus múltiples variantes: compartidas, enlazadas, virtuales, entrelazadas, etc. En el modelo de MENTAL, se avanza desde las expresiones simples a las complejas.
Complejidad.
Con MENTAL se explica la complejidad como aplicación recursiva de reglas simples, como con el juego de la vida. MENTAL, como el juego de la vida, muestran que la vida puede tener un origen simple.
Simulación.
Los modelos son abstractos y pueden implementarse en un ordenador cuyas primitivas son precisamente las mismas con las que se construyen los modelos. Al ser MENTAL el lenguaje formal más próximo a la conciencia, es el mejor lenguaje para simular los fenómenos de los sistemas vivientes.

MENTAL es la demostración de que unos principios globales o generales (las primitivas) y unas leyes particulares locales producen algo que se asemeja a la vida.
Abstracción.
Las primitivas semánticas representan el supremo nivel de abstracción. MENTAL es la máxima aproximación posible al tema de la VA, de la misma manera que a la IA, a la conciencia y a la semántica. La abstracción cubre los niveles físico, mental y vital.
Principios.
Para Ed Fredkin, los mismos principios rigen para el universo que para los organismos vivos que lo habitan. Estos principios comunes son precisamente los arquetipos primarios, los arquetipos de la conciencia.
ACs.
No se necesita apoyarse forzosamente en los ACs, de comportamiento local. También pueden haber interacciones no-locales. Los ACs son un subdominio de aplicación de MENTAL, con un entorno especial restringido y expresiones restringidas también. Los ACs y el juego de la vida son universos por explorar, como MENTAL.
Entidades.
Pueden definirse entidades virtuales a partir de la entidad principal. Las entidades virtuales serían como vistas o derivaciones de la entidad principal.

Pueden definirse todo tipo de entidades imaginarias o virtuales, solo limitada por los grados de libertad. Podemos modelar fácilmente toda clase de procesos biológicos.

En MENTAL, la vida virtual y la sintética se confunden, pues sintetizamos (de forma análoga a la química) entidades abstractas mediante las primitivas.
Fundamentación.
MENTAL aporta una fundamentación a la VA. Permite clarificar el proceso de la vida al contemplarla desde un nivel profundo, el de los arquetipos primarios. Como los fenómenos biológicos son muy complejos, acudimos a la abstracción y a la generalización para entenderlos.

Las primitivas de MENTAL son el ADN de todo lo existente. Es el modelo universal subyacente a toda forma de vida. MENTAL es el genotipo universal, el ADN. El fenotipo son las aplicaciones.

Por su supremo nivel de abstracción, MENTAL hace que la frontera entre la IA y la VA se diluya, pues ambas tienen la misma fundamentación. MENTAL es transdisciplinario.
Diversidad.
La diversidad de expresiones se producen por combinatoria del ADN básico (las primitivas), como ocurre con los seres vivos.
Creatividad.
MENTAL es creativo. La creatividad se produce de forma discontinua, por saltos. La evolución se contempla como la búsqueda de combinaciones creativas.
Libertad y conciencia.
Características de la vida son la libertad y la conciencia. Las primitivas de MENTAL son arquetipos de la conciencia y grados de libertad.

El juego de la vida. Analogías con MENTAL

El hecho de que el juego de la vida genera tal diversidad de formas posibles indica que se trata de algo profundo, próximo a un arquetipo. Cuanto más profundo es un arquetipo, mayores son sus manifestaciones. Es por esta razón por la que despertó tanto interés y la razón de que tenga connotaciones filosóficas. En este sentido, guarda ciertas analogías con MENTAL, por su simplicidad, por la infinidad de formas potenciales que puede generar, porque es un modelo computacional ,y porque integra información y entorno.

Las reglas del juego de la vida se sitúan en la frontera entre la baja población y la alta población de células.
Une los opuestos. Une simplicidad y complejidad. Actúa en la frontera entre orden y caos. Une lenguaje formal y lenguaje visual (geométrico), pues genera comportamiento cualitativo observable. El propio tablero de celdas une también los opuestos de blanco y negro.
Es iniciático. Activa la imaginación y la conciencia. Muchas personas que lo ven por primera vez quedan sorprendidas y cautivadas, deseando experimentar por sí mismas.

Guarda también analogía con el programa de generación de mándalas, pues unos elementos geométricos simples generan una diversidad infinita de formas. Aunque en el caso de los mándalas las imágenes son estáticas.

Codificación en MENTAL del juego de la vida


// Asignamos un valor “0” a una célula muerta (blanca) y “1” a una célula viva (negra).



// c1 es la matriz bidimensional de células de n×n elementos.



// c2 es la matriz en el instante siguiente.



// valores inciales



(n = 1000)  // semidimensión (horizontal y vertical) de la tabla de celdas


(m = 1000)  // número de iteraciones



(k = [−n…n]°)



[(c1(k k) = 0)]  // poner inicialmente la matriz a ceros



( c1(00) = 1 )  // configuración inicial de células vivas



...



presentar(c1)  // presentar c1 en pantalla



⟨( vecinas(i j) = c1(i j+1) + c1(i j-1) +


                     c1(i-1 j) + c1(i+1 j) + 


                     c1(i-1 j-1) + c1(i-1 j+1) +


                     c1(i+1 j-1) + c1(i+1 j+1) )⟩



// bucle (m iteraciones)



	[ (i=[1…m])



      [i=k j=k



     ( (c1(i j) = 1) → (vecinas(i j) = ⌊2 3⌋) →



                           (c2(i j) = c1(i j)) )



     ( (c1(i j) = 0) → (vecinas(i j) = 3) →



                        (c2(i j) = 1) )



     ( (c1(i j) = 1) → (c2(i j) = 0) )



  ]



  [ i=k j=k (c1(i j) = c2(i j)) ]  // hacer c1 = c2



presentar(c2)  // presentar c2 en pantalla



]

Un criterio que también se puede utilizar para saber si se ha llegado a una configuración estable es que ver si los tableros c1 y c2 son iguales.

Respecto al tema de la autorreproducción de una máquina, este proceso es muy complejo si se basa en reglas locales, de transición continua. En cambio, si se basa en reglas no-locales, la solución es discontinua y muy sencilla. Basta con especificar una regla de transformación que copia la configuración inicial sobre otra zona del tablero definida por el vector (dx dy).

Bioformas vs. Mandalas

Las bioformas de Dawkins tienen reglas de desarrollo locales, es decir los cambios son pequeños o graduales que se producen de una generación a la siguiente. De cambios locales acumulados pueden emerger una gran variedad de formas complejas. Lo mismo ocurre con el juego de la vida de Conway, que también utiliza reglas locales y que también pueden producir muchas formas dinámicas complejas. El hecho de que se produzcan tal variedad de formas (superficiales), indica que también estamos ante algo próximo a un arquetipo (profundo).

El programa (B) que genera las bioformas guarda ciertas analogías con el programa (M) que genera los mándalas que ilustran este libro:

B utiliza solo rectas. M utiliza rectas, círculos y polígonos regulares. Ambos evocan arquetipos geométricos.
B utiliza como mecanismo recursivo la ramificación. M utiliza la ramificación y otros mecanismos adicionales como reducción, persecución, etc.
Los dibujos de B tienen simetría izquierda-derecha. Los dibujos de M tienen simetría circular.
Ambos programas tienen parámetros (que se llaman genes en el caso de B), que son los grados de libertad, con los que se pueden generar potencialmente infinitas formas.
B se enfoca en las formas de vida. M se enfoca en los mandalas, que son manifestaciones de la conciencia.
Ambos programas pueden producir formas emergentes imposibles de prever a priori (antes de la ejecución), que pueden ser simples o complejas.

Adenda
La fundación de la VA

La VA nació oficialmente como disciplina independiente en 1987 en la International Conference on the Synthesis and Simulation of Living Systems, también conocida como “Articial Life I” o “ALIFE I”, que tuvo lugar en el Los Alamos National Laboratory, de Santa Fe (Nuevo Mexico). Acudieron más de un centenar de científicos de diferentes disciplinas como biología, informática, física, filosofía y antropología. El evento fue apoyado por el Santa Fe Institute, una entidad privada dedicada a la investigación interdisciplinar en Sistemas Complejos. LA VA se considera un área de investigación que está dentro de los Sistemas Complejos. El promotor de la reunión fue Christopher Langton, que fue el primero en introducir el término “vida artificial”.

Langton ha investigado los ACs en sus aspectos cualitativos mediante la evaluación de los comportamientos emergentes. En este aspecto, ha estudiado “La vida al borde del caos” −título de su tesis doctoral− en los ACs basándose en la noción de entropía. Encontró comportamientos simples (que alcanzan configuraciones fijas o periódicas en pocos pasos), complejos (que convergen en periodos largos) y caóticos (que no producen formas definidas). Postuló que los comportamientos complejos evolutivos se dan en un estrecho margen de circunstancias específicas. También ha investigado el tema de los modelos de máquinas auto-replicativas.

Más sobre el juego de la vida

Conway experimentó inicialmente el juego de la vida con la ayuda del juego del Go, que es tablero formado por líneas horizontales y verticales sobre cuyas intersecciones se colocan fichas blancas o negras, que corresponden respectivamente a dos jugadores. Pero pronto se inventaron los ordenadores personales y pasó a experimentar con ellos. El juego del Go también le sirvió de inspiración a Conway para inventar los números surreales.

El juego de la vida se dió a conocer en Octubre de 1970 en una columna de Martin Gardner de Scientific American. El artículo despertó un gran interés. Con la introducción de los ordenadores personales, la gente empezó a experimentar con diversas formas iniciales, descubriéndose muchas estructuras interesantes: el pentominó r; patrones que crecen indefinidamente como las pistolas (guns), que generan planeadores; deslizadores (gliders); locomotoras (puffers) que se mueven y dejan un rastro de basura; rastrillos (rakes) que se mueven y emiten naves espaciales; explosionadores; etc.

El 18 de Mayo de 2010, Andrew J. Wade descubrió un patrón autorreproductor (al que denominó “Gemini”). Este patrón se replica tras 33.6 millones de generaciones. En cada réplica elimina al padre.

Se conocen muchas variantes del juego de la vida. El juego estándar se simboliza por S23/B3 (2 o 3 células vivas vecinas son necesarios para sobrevivir y 3 células vivas son necesarias para que una célula vuelva a vivir). Por ejemplo, la versión S16/B6 indica que una célula sobrevive si tiene 1 a 6 vecinas y necesita 6 vecinas para revivir. El juego S12/B1 genera varias aproximaciones al triángulo de Sierpinski cuando se aplica a una sola célula viva.

Se han desarrollado también versiones con malla hexagonal o triangular y con más de dos estados (que se representan con colores). Hoy día hay cientos de programas y versiones online del juego de la vida.

Tom Ray y la VA

Tom Ray es un biólogo que estuvo buscando el secreto de la evolución de la vida en el mundo real. Primero la buscó en Costa Rica, estudiando las mariposas y las hormigas. Pero esta investigación la encontró bastante frustrante, pues quería ser capaz de observar sus efectos sobre miles de generaciones de organismos. Finalmente encontró lo que buscaba en el departamento de IA del MIT. El descubrimiento de Ray fue que los programas pueden actuar como organismos vivos: interactuando, autorreplicándose, sufriendo mutaciones al azar y pasando un código a sus hijos. Ray aprendió programación genética, y un día nacieron sus primeras “criaturas digitales”. El espacio donde habitaban estas criaturas virtuales lo denominó “Tierra” (en español), una simulación por ordenador de la evolución de la vida, con mutaciones, herencia y selección natural.

Turing y la VA

Alan Turing −que concibió un dispositivo abstracto que hoy conocemos como “máquina de Turing universal” capaz de procesar cualquier algoritmo, y que es el fundamento de los ordenadores− fue también un pinero en lo hoy denominamos “vida artificial”. Murió cuando estaba trabajando en la simulación informática de los procesos de desarrollo biológico.

Bibliografía

Álvarez López, José. Bioinformática. Bases para una nueva biología. Espacio y Tiempo, 1992.
Attwood, Teresa; Parry-Smith, David. Introducción a la Bioinformática. Pearson Alhambra, 2002.
Bohm, David; Peat, F. David. Ciencia, orden y creatividad : las raíces creativas de la ciencia y la vida. Kairós, 2010.
Emmeche, Claus. Vida simulada en el ordenador. La nueva ciencia de la vida artificial. Gedisa, 1998.
Fernández, Julio. Vida artificial. Ediciones de la Universidad Complutense de Madrid, 1992.
Jenkins, Lyle. Biolingüística. Cambridge University Press, 2002.
Langton, Christopher (ed.). Artificial Life. SFI Studies in the Sciences of Complexity. Addison-Wesley, 1988.
Lahoz Beltrá, Rafael. Bioinformática. Simulación, vida artificial e inteligencia artificial. Díaz de Santos, 2004.
Levy, Steven. Artificial Life. A report from the frontier where computers meet biology. Vintage, 1992.
Prata, Stephen. Vida artificial. Anaya Multimedia-Anaya Interactiva, 1994.
Ramos Salavert, Isidro. Vida artificial. Universidad de Castilla-La Mancha, Servicio de Publicaciones, 1995.
Rayo, Agustín. El juego de la vida. Investigación y Ciencia, Diciembre 2010.
Smith, Justin E.H. Divine Machines: Leibniz and the Sciences of Life. Princeton University Press, 2011.
Solé, Ricard. Vidas sintéticas. Una aproximación revolucionaria a la ciencia, la historia y la mente. Tusquets Editores, 2012.
Stewart, Ian. Las matemáticas de la vida. Crítica, 2011.
Stewart, Ian. El segundo secreto de la vida. Crítica, 2006.
Sullins III, John P. Gödel incompleteness theorems and artificial life. Internet.
Thompson, D’Arcy. Sobre el crecimiento y la forma. Akal, 2011.
Von Neumann, John. Theory of self-reproducing automata. University of Illinois, 1996.